📌 Initialization의 필요성
파라미터들의 시작 위치가 전역 최소점에 가까울수록 빠른 수렴이 이루어짐
따라서 손실 함수에서 매개변수의 적절한 시작 위치를 결정하는 것은
전역 최소점 수렴에 대한 지름길이며, Vanishing Gradient 문제의 해결 방법이 될 수 있음
📌 Vanishing Gradient란?
역전파 과정에서 기울기가 극도로 작아지는 현상을 의미하며, 파라미터가 충분히 업데이트되지 않음

주로 Sigmoid, Tanh의 활성화 함수에서 해당 문제점이 발생함

위의 파란색 그래프가 기울기인데,
대부분 1보다 작은 값을 지니기 때문에 미분값을 곱할 경우 기울기가 계속하여 작아짐
즉, 왼쪽으로 갈 수록 기울기가 소멸되는 현상 발생
ReLU의 활성화 함수의 경우

음수값에서의 기울기 소멸 문제 발생
이에 대한 대응으로 음수값에 기울기를 주는 Leaky ReLU가 존재
📌 Exploding Gradient란?
큰 기울기로 인해 매우 큰 업데이트가 발생하는 문제
Gradient Clipping이라는 해결책 존재
일정 임계값보다 클 경우를 고려하여 아래와 같은 식 사용

📌 Initial Weights가 큰 랜덤 변수일 경우
Sigmoid, tanh → Vanishing Gradient Problem 발생

ReLU or Leaky ReLU → Exploding Gradient Problem 발생
[ 🚨 ]
즉, 초기 가중치를 너무 크게 두면 안됨
📌 Initial Weights가 작은 랜덤 변수일 경우
만약 모든 가중치의 초기 변수가 0에 가까울 경우, 내적의 결과 또한 아주 작게 되어 업데이트 발생 X

[ 🚨 ]
즉, 초기 가중치를 너무 작게 두면 안됨
📌 Initial Weights가 상수일 경우
계산 식이 같아 동일한 업데이트가 이루어짐
→ 노드가 여러개인 이유가 사라짐
[ 🚨 ]
즉, 초기 가중치를 하나의 상수로 두면 안됨
📌 Xavier Initialization
데이터가 분산을 유지하면서 흘러가도록 하며 초기화하는 방식

위 그림처럼 활성화함수에서 기울기가 있는 곳을 통과하도록 노력
➡️ 결과적으로 Gradient Vanishing이 사라져 신경망의 학습이 잘 진행됨
[ 🚨 ]
그러나 활성 함수가 ReLU일 때, Xavier 초기화를 적용해보면, 입력 데이터가 계층을 통과하면서 분산이 점점 줄어들어 출력이 0이 되는 현상 발생 (ReLU의 비활성화부분 존재)
📌 He Initialization
ReLU 사용시, 출력의 분산이 절반으로 줄어들기 때문에 가중치의 분산을 두 배로 키움
즉, Xavier 초기화는 가중치의 분산을 1/n로 하였다면, He 초기화는 가중치의 분산을 2/n으로 함
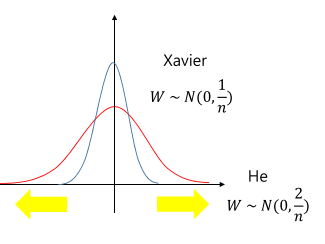
➡️ 위와 같은 방법을 통해 ReLU에서도 적절한 초기화 가능



