📌 통신에서의 Convolution
두 신호중 하나의 신호가 움직여가며 신호의 overlap되는 부분의 면적이 output이 됨
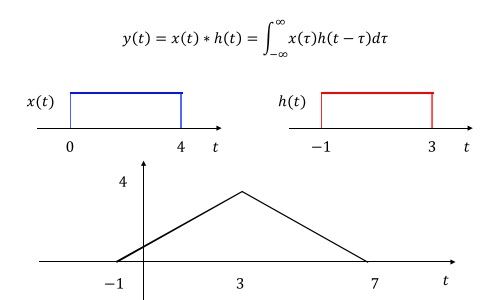
인공지능에서의 Convolution은 통신에서의 합성곱과 비슷한 개념으로 받아들일 수 있음
📌 Image (2D) Convolution

Window의 이동을 통하여 입력 이미지를 대표할 수 있는 입력변수로 만들어나가는 하나의 방식
ex)
Window 내의 수들의 합을 구하여 대표하는 pixel 생성
Window 내의 수들과 Window의 계수들의 내적을 구하여 대표하는 pixel 생성
Window를 통과한 숫자들을 Filter Coefficients를 활용한 Convolution으로 새로운 pixel을 생성한다고 보면 됨
『
Window : Filter가 바라보는 영역
』
📌 Filter Coefficients
입력 픽셀과 Filter Coefficients의 컨볼루션을 기반으로 새로운 픽셀 생성
주어진 필터 계수를 사용하여 Edge Detection, low-pass filtering 등의 task 수행
신경망 훈련 중 학습 가능한 계수 (목적에 따른 학습)
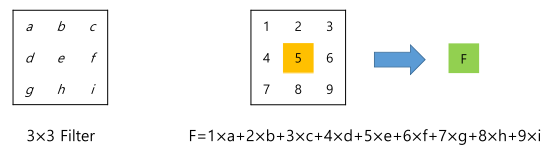
『
필터 하나당 한개의 bias를 지님
』
📌 Sobel Filter
기울기 크기 계산을 위한 한 쌍의 3×3 컨볼루션 필터로,
수평 및 수직 방향의 기울기 성분을 별도로 계산할 수 있음
아래와 같은 필터의 형태를 띔

위 Sobel Filter : 세로 성분을 찾아줌
아래 Sobel Filter : 가로 성분을 찾아좀
즉, 더한 값을 봤을 때 상하, 좌우의 차이를 찾아 기울기 성분 계산
➡️ Edge Detection에 활용 가능
(Sobel Filter를 활용한 Edge Detection 실습은 다음 포스트로 업로드 예정)
📌 Stride
컨볼루션의 각 단계에서 몇 step을 이동할지 결정하는 Parameter
[ 🚨 ]
큰 입력 이미지(화질이 좋은 입력 이미지)의 경우, pixel 하나하나 사이의 연산을 수행하게 되면 비용이 많이 듦
또한 큰 이미지일수록 pixel 하나하나의 중요도가 낮을 것으로 예상됨
➡️ 이미지를 듬성듬성 보자

위와 같이 건너뛰며 연산함으로써, 복잡도를 줄일 수 있음
📌 Padding
입력 이미지나 특징 맵의 경계를 추가하여 해상도를 확장하는 Parameter
[ 🚨 ]
바깥쪽 pixel들의 경우, 공평하게 훑을 수 없으며
사이즈를 줄이고 싶지 않을 때에도 사이즈가 줄어들 수밖에 없는 상황 발생
➡️ 이미지의 바깥쪽 pixel들까지 훑을 수 있도록 이미지 확장

📌 Dilation
연속된 계수 사이에 구멍을 삽입하여 필터를 확장하는 Parameter
앞에까진 이미지와 관련되었다면, Dilation은 필터를 직접 팽창시킴
보고자 하는 영역을 키움
만약 3 * 3 필터를 가지고 있다면, 사이사이에 2개의 빈 값을 두어 마치 7 * 7필터의 효과를 봄

📌 Input & Output Size
이들을 모두 고려하여, 다음과 같은 식으로 최종 Input Size 및 Output Size를 계산하여 구할 수 있음

📌 3D Convolution
위와 동일한 개념이나, 한 축이 더 늘어났다고 보면 됨 (채널의 개념 등장)
예를들어 아래의 사진에서 R, G, B로 세개의 채널이 존재한다고 할 수 있음
이때,
Ci = Cf / C0 = N으로 차원을 잘 맞출 수 있어야 함

예를들어

Sobel Filter에서 x, y 두개의 필터를 둔다면 output은 두개의 채널을 지님
또한 R, G, B의 세개의 입력 채널을 가지고 있다면, 필터의 채널도 3이 될 것



