컴퓨터 그래픽스를 공부하기 위해서는 좌표계의 이해 및 수학적 사전 지식이 필요함
점으로 선을 구성하고, 선으로 면을 구성하며 다양한 면을 사용하여 물체를 구성하기 때문
📌 VECTORS
point : 점
vectors : 방향과 크기가 있는 물리량 (상대위치 상관 X, 좌표계에 독립적임)
unit vector : 방향만을 나타내는 단위벡터
스칼라 : 양
『
상대 위치와 좌표계를 기준으로 하는 물리량은 독립적이지 못하고 상대적임
』
📌 POINT or VECTOR ?
point들과 vector들의 연산이 이루어진 후의 결과는 point일까 vector일까?
point + vector = point : 포인트를 벡터의 방향과 크기로 이동한다는 개념
vector + vector = vector : 벡터간의 합/차
point - point = vector : 점과 점 사이의 방향성과 크기가 결과
point + point = not defined
📌 Dot product (or inner product)
그래픽스에서의 내적은 해당 위치의 받는 빛의 양을 계산할 때 많이 사용됨
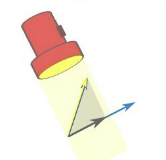
이때, 크기가 같고 수직인 벡터를 해당 벡터의 normal vector라고 하며,
두 normal vector간의 곱은 0 (오른손 법칙을 사용하여 구할 수 있음)
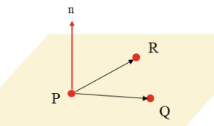
📌 Cross product
그래픽스에서의 외적은 면의 법선 벡터를 구하여 빛 등의 반사를 계산할 때 많이 사용됨
📌 선의 정의
- 두 점
- 한 점과 선에 평행한 벡터
- 한 점과 선에 수직인 벡터
위 정의에 각각 대응되어 선을 표현하는 세 가지 수학적 표현 존재
- explicit equation : 계산량이 높으며 3차원 이상 X / 기울기 구하듯 계산
- parametric equation : line(t) = vt + p0 / 즉, t 하나만 계산하면 선이 정해짐 / 제일 간단하며 확장성 높음
- implicit equation : 내적하여 0이 되도록 / 차원을 높혀도 사용이 가능함
📌 행렬
행과 열로 구성된 요소 집합 (벡터 또한 행렬의 일부)
Orthgonal : 완전한 선형 독립 (직교성)
그래픽스는 직교 좌표계 사용
'[그래픽스]' 카테고리의 다른 글
| [그래픽스] OpenGL 카메라 : 평행 관측, 투시 관측, 투영 (0) | 2024.02.07 |
|---|---|
| [그래픽스] CTM이란?, OpenGL Coordinate System 실습 (2) | 2024.02.07 |
| [그래픽스] Transformations : Rotation, Scaling, Reflection, Inverse, Transformation의 순서, 변환 순서 (2) | 2024.02.07 |
| [그래픽스] 데카르트 기하학, 아핀공간, 동차좌표계 (0) | 2024.02.06 |
| [그래픽스] OpenGL이란? : OpenGL입문, 매트릭스모드, polygon의 조건, z-buffer (1) | 2024.02.05 |



