[선형대수학] 선형방정식 기초의 이해 : 선형방정식과 선형시스템, 선형방정식의 기하학적 표현, 가우스 소거법, 가우스-조던 소거법

 

📌 선형(Linear)

: 집합 A의 원소들에 대해 선형결합의 형태로 나타낼 수 있는 것

즉, 집합 A의 원소들에 각 상수를 곱하여 더한값들이 A에 속하는 경우 (선형결합, 1차결합)

ex)

 

 

📌 선형방정식과 선형시스템

“선형방정식을 푸는 것”이 매우 중요함

• 과학, 산업적 응용 등 다양한 분야에서 선형방정식 문제를 만나는 경우 多
• 복잡하고 어려운 문제들을 선형방정식 문제로 축약시킬 수 있는 경우가 흔히 존재

 

선형방정식은 변수들의 곱이나 제곱근 형태를 포함하지 않는 방정식

모든 변수는 1차항까지만 포함하며, 다차항, 삼각, 로그, 지수함수 등을 포함한 식은 선형방정식이 될 수 없음

 

선형시스템은 변수에 관한 유한개의 선형방정식의 집합

모든 해의 집합을 해집합이라고 함

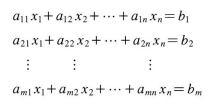
이들 식에서 a, b값들이 알려졌을 때 위의 식을 만족시키는 x값들을 구하게 되는데, 이를 해라고 하며 모든 해의 집합을 해집합이라고 함

 

만약 모든 b값이 0인 경우, 위의 식을 동차선형시스템이라고 함

이때, 모든 x가 0인 경우 이 동차선형시스템의 해가 되는데 이러한 경우를 자명해라고 함

또한 이 동차선형시스템에서 하나의 x라도 0이 아닌 경우의 해를 비자명해라고 함

 

선형방정식들이 똑같은 해를 가질 때 두 식이 동치라고 함

 

 

📌 선형방정식의 기하학적 표현

선형방정식의 해를 기하학적으로 나타내면, 그래프의 교차지점을 의미함

⬇️ 2차원 공간에서의 해

⬇️ 3차원 공간에서의 해

이때, 3차원을 넘는 공간에서는 우리 눈에 잘 보이지 않기에 통상 2개나 3개의 변수를 보는 것에 국한됨

 

 

📌 선형방정식의 소거법

: 선형시스템에서 해를 구하는 방법 중 하나

원래의 시스템과 동치이면서도 해를 더 쉽게 구할 수 있도록 변형해나아가는 과정

우리가 무의식중에 수행하던 연립방정식과 비슷

 

가우스 소거법

다음과 같은 3가지 기본 연산에 의해 원래의 식과 동치인 선형방정식으로 변환 가능

• 한 방정식에 0이 아닌 상수를 곱한다.
• 방정식들의 위치를 서로 교환한다.
• 한 방정식에 0이 아닌 상수를 곱하여 다른 방정식에 더한다.

 

가우스-조단 소거법

• 전향 소거법 : 각 방정식에 다른 식의 변수들을 계수와 반대가 되도록 적절한 상수를 곱하여 두 식을 더함으로써 해당하는 변수들을 차례로 소거한 새로운 방정식 L을 구한다.
• 역대입법 : 새로운 방정식 L로부터 하나의 변수 값을 구한 후 남은 식들에 차례로 대입하여 전체 해를 구한다.

 

전향 소거법과 역대입법 과정을 합하여 가우스-조단 소거법이라고 하며, 전향 소거법을 가우스 소거법이라고 함

즉, 역삼각형의 꼴로 식을 정리하여 알 수 있는 변수부터 대입해가며 모든 변수의 해를 구하는 방식

ex)

⬇️

이때, 과정에서 모순이 발생하였을 경우 해당 선형시스템은 해를 가지지 않는 것으로 간주