[인공지능] Optimization, 최적화란? Optimizer의 발전 과정 : GD, SGD Momentum, Nesterov Momentum, Adagrad, RMSProp, Adam

 

📌 Optimization이란?

loss함수의 최소값을 찾아가는 것

 

 

📌 Optimizer의 발전

Optimizer는 우리가 아는 Gradient Descent에서 시작되어 다양한 방향으로 발전함

어떤 점들을 개선해나아갔는지 하나하나 알아보자

 

 

📌 Gradient Descent의 문제점

앞선 포스트에서 Gradient Descent에 대해 다루며, 가중치를 업데이트해가는 방향을 설명했음

[인공지능] Backpropagation, 역전파란? Gradient Descent 경사하강법이란? Backpropagation 실습

그러나 Gradient Descent에는 다양한 문제점 존재

 

[ 🚨 ]

Batch GD : 수렴 경로가 올바르게(loss가 낮아지게) 유지되나, 계산복잡도가 높음

SGD : 수렴 경로가 복잡하지만 수렴 속도가 빠르고 메모리 요구 사항이 낮음

전역 최소점에 도달하기 위해 멈출 수 있는 Local Minimum 및 Saddle Point 문제

 

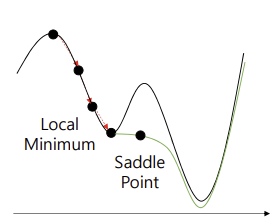
➡️ 이전의 방향성과 빠르기를 고려하여 이러한 문제점을 해결하자

 

 

📌 SGD Momentum

이전의 속도 이력을 기반으로 Momentum 계산하여 파라미터 업데이트에 이를 적용

➡️ Gradient Descent의 문제점인 느린 학습을 해결하고, 안장점을 탈출하며 진동을 방지

 

아래와 같이 Vk의 과거 이력을 계산식에 적용하여 파라미터 업데이트 수행

 

[ 🚨 ]

Overshooting 문제점 발생

누적된 기울기로 인해 전역 최소점(우리가 찾고 있는 점)을 초과함

전역 최소점 주변의 경사가 가파를 경우, 해당 문제가 발생할 수 있음

 

➡️ 현재 속도 계산량 + 앞으로 이동 할 속도 계산량을 고려하여, 오버슈팅 여부를 살펴본 후 교정하자

 

 

📌 Nesterov Momentum

앞으로 이동 할 기울기까지 고려해본 후, 얼마나 이동할지 결정하는 알고리즘

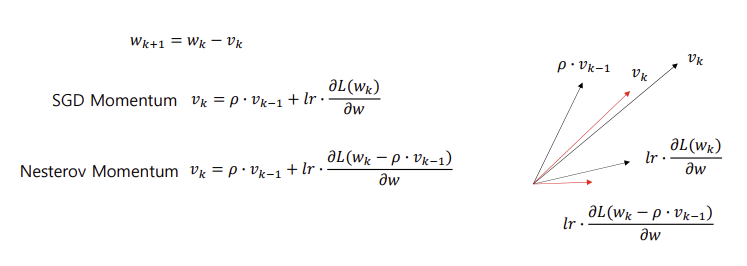
앞으로 이동 할 기울기로 인해 어떻게 될 지 고려 (overshooting 여부를 확인)

➡️ 절반 정도 이동한 후 어떤 방식으로 이동할지 다시 계산하여 스텝을 결정함으로써 단점 극복

 

『

모멘텀 : 모멘텀 값 + 기울기 값

네스테로프 모멘텀 : 모멘텀 값이 적용된 지점에서의 기울기 값

』

 

 

📌 AdaGrad (Adaptive Gradient)

Learning Rate를 상황에 맞게 변화

1. 이제까지 많이 움직였으면 지금부터는 LR을 적게 하여 조금 움직이자
2. 기울기의 크기가 크다면, LR을 적게 하여 발산을 막자
3. 처음부터 기울기가 너무 크다면 전역 최소점과 가깝다고 판단하자

이때, Gk : 이제까지 온 기울기들의 제곱의 합

 

[ 🚨 ]

Gk가 잘못 누적될 경우, 정작 필요한 곳에서 많이 못 갈 수 있음

안장점을 통과하기 쉽지 않으며 수렴이 느려짐

즉, 학습률이 계속하여 감소되어 조기 학습 중단 문제 발생

 

➡️ Gk를 막기 위한 스케일링을 해주자

 

 

📌 RMSProp (Root Mean Square Propagation)

Gk는 누적되는 값으로, 커지는 값

즉, 갑자기 커질 경우 줄지 않으며 무조건 학습률은 떨어지게 됨

➡️ 앞에 1 미만의 값(r)을 곱해주어 스케일링 수행하여 조기 학습 중단의 문제 해결

 

『

미분값이 큰 곳에서는 업데이트 할 때 큰 값으로 나누어주기 때문에 기존 학습률보다 작은 값으로 업데이트 됨

즉, 진동을 줄이는 데 도움이 됨

반면 미분값이 작은 곳에서는 업데이트시 작은 값으로 나누어주기 때문에 기존 학습률보다 큰 값으로 업데이트 됨

이는 조기 종료를 막으면서도 더 빠르게 수렴하는 효과를 불러옴

』

 

[ 🚨 ]

출발 지점에서 멀리 떨어진 곳으로 이동하는 초기 경로의 편향 문제 발생

위 식에서의 Gk가 매우 작아지기 때문

 

➡️ 새로운 식을 적용하여 초기 경로의 편향 문제를 제거하자

 

 

📌 Adam (Adaptive Momentum)

Adam = Momentum + RMSProp

실제로 현재 가장 많이 사용되는 Optimizer로, 진행하던 속도에 관성도 주고, 최근 경로의 곡면의 변화량에 따른 적응적 학습률을 갖는 알고리즘

 

이때, 아래의 식을 적용하여 식의 상쇄를 활용해 G1은 기울기의 제곱이 되어 아주 작아질 일이 없음

 

➡️ RMSprop의 단점인 초기 경로의 편향 문제 해결

 

『

Hyper parameter

앞서 지켜본 Optimizer와 비교하여 Hyper parameter가 많음

• lr : 학습률. 매우 중요하고 보정될 필요가 있으므로 다양한 값을 시도해서 잘 맞는 값을 찾아야 합니다.
• β1 : 기본적으로 0.9를 사용 / 도함수의 평균을 계산하므로 첫 번째 momentum
• β2 : 기본적으로 0.99나 0.999를 이용(논문에서는 0.999를 추천) / 지수 가중평균의 제곱을 계산하므로 두 번째 momentum
• ϵ : Adam 논문에서는 10−8을 추천. 분모가 0이 되는 것을 막기 위해 더해주는 상수. 하지만 이 값을 설정하지 않아도 전체 성능에는 영향이 없습니다.

보통 β1, β2, ϵ의 세 가지 값은 고정 시켜두고, lr를 바꿔보며 최적의 값을 찾음

』