[인공지능] 선형회귀(Linear Regression) 실습 : 선형회귀란? 경사하강법이란? 선형회귀, 경사하강법 적용 파이썬 코드
📌 선형회귀
: 독립 변수와 종속 변수 간의 관계를 표현하여 기존의 데이터에 없던 새로운 값을 예측

기존의 여러 데이터를 대표할 수 있는 회귀식 필요
이해를 위해, h(x) = Wx + b의 일차식 형태로 가정
이 회귀식이 기존의 여러 데이터를 얼마나 잘 표현하는지 판단의 척도(손실함수) 필요
손실함수는 예측값-실제값의 제곱의 합의 평균의 형태로 작성
이 손실값을 최소화하는 방향으로 성능 향상
손실함수의 경우, Wx + b를 이론에 대입하여 구해보면 아래와 같이 이차식으로 표현됨

우리의 목적 : 손실을 줄이는 W를 찾아 최대한 정확한 예측을 수행하는 것
초기 예측한 W값에서 손실함수의 최저점에 도달하도록 값을 옮겨나가는 작업이 필요함
➡️ 이렇게 옮겨나가는 작업 : 경사하강법
📌 경사하강법
기울기(Gradient Descent)를 하강(Descent)시키는 과정
W의 이동에 따른 손실함수의 변화량(기울기)를 알아야 함
이를 확인한 후 기울기를 0에 도달하도록 알맞은 방향으로 W를 이동

이때, 기울기를 줄여나가기 위한 움직임의 정도를 조정하기 위한 학습률 존재
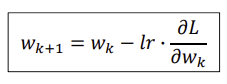
위와 같이 기울기에 학습률을 곱한 값을 빼주어 W값을 조정해나감
(양수이면 작게, 음수이면 크게, 절댓값이 크면 많이, 작으면 적게 등 고려)
이에 따라 학습률은 너무 크면 발산하고 너무 작으면 도달하기까지 너무 오래 걸리기에
여러번 확인하며 적절한 값을 잘 골라줘야 함

실제 손실함수에 따른 변화량 계산시 손실함수가 위와 같을 때,
W, b값에 따른 손실함수의 변화량을 다음과 같이 구할 수 있음


이를 위의 식에 대입하여 W, b 조정 (아래 실습 코드 참고)
『
“Mini-Batch, Epoch, Iteration”
Mini-Batch (미니배치)
- 한 번의 학습에서 전체 데이터셋을 나누어 처리하는 작은 데이터 그룹
- 신경망 모델을 조금씩 업데이트하는 데 사용
Epoch (에포크)
- 전체 데이터셋을 한 번 학습하는 과정
- 신경망이 전체 데이터셋을 한 번 훑고 학습을 완료하는 시점
Iteration (반복)
- 한 번의 에포크 동안 신경망이 미니배치 단위로 학습을 수행하는 횟수
- 각 반복은 미니배치의 데이터를 사용하여 가중치를 업데이트하는 단계를 나타냄
➡️ 위와 관련된 값을 설정해나아가며 경사 하강법의 종류가 달라짐

Batch GD - 안정
- 전체를 보고 신중히 결정
- 네트워크에 모든 샘플을 다 넣어서 계산 (m = 10)
Stochastic GD (SGD) - 불안정
- 하나씩만 막 보고 결정하므로 불안정
- 한번 훑을 때, 10번의 업데이트 (m=1)
Mini-batch - 중간
- 한번에 다 넣어서 계산이 힘들지도 않게 하고, 하나하나 다 봐서 불안정하게 하지도 말자
- GPU가 한번에 수용할 수 있는 양만큼 batch를 정하여 (최대한 크게) 안정적으로 네트워크 업데이트
- 특정 크기 마다 업데이트 (m = n)
』
📌 선형회귀 실습
“키를 바탕으로 몸무게를 예측할 수 있는 회귀선을 그려보자”

위의 Height, Weight 데이터프레임을 바탕으로 선형회귀 실습 진행
x : Height / y : Weight
⬇️ 선형회귀 실습 코드
import numpy as np
w = 0
b = 0
epoch = 4000000
lr = 0.00005
for i in range(1, epoch): # epoch만큼 반복
# w와 b에 따른 손실함수 변화량 업데이트
w_diff = 2 * np.mean((w*x["H"] + b - y["W"])*x["H"])
b_diff = 2 * np.mean(w*x["H"] + b - y["W"])
# 해당 계산을 바탕으로 w, b값 업데이트
w -= (lr * w_diff)
b -= (lr * b_diff)(이때, w와 b가 0으로 시작했으므로 필요한 값을 찾아나가기 위해 많은 에포크와 적은 학습률 필요)
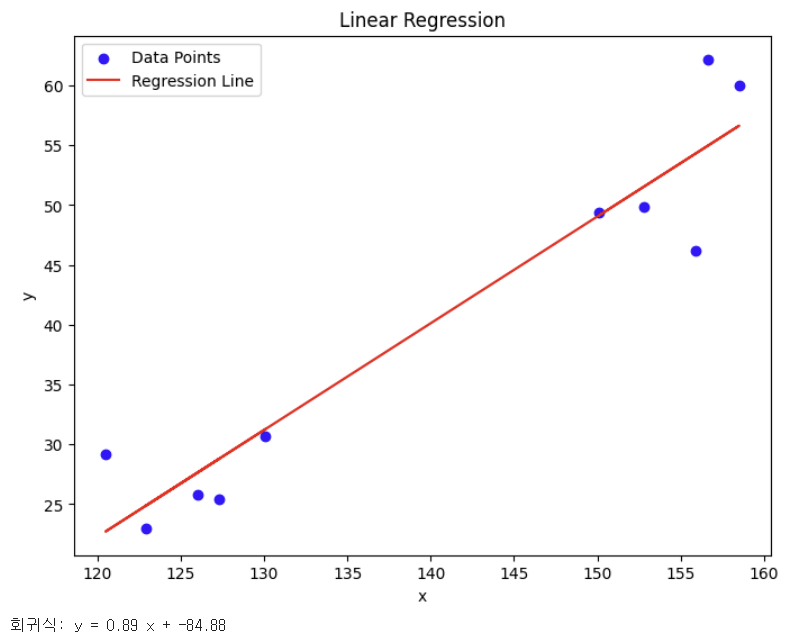
⬇️ 선형회귀 실습 결과 시각화
import matplotlib.pyplot as plt
# 회귀식 시각화
plt.figure(figsize=(8, 6))
plt.scatter(x["H"], y["W"], color='blue', label='Data Points') # 입력 데이터 포인트 시각화
plt.plot(x["H"], w * np.array(x["H"]) + b, color='red', label='Regression Line') # 회귀선 시각화
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.title('Linear Regression')
plt.show()
print("회귀식: y =", round(w, 2), "x +", round(b, 2))