[인공지능수학] 다양한 수학적 개념들이 인공지능에 어떻게 활용될까? : 행렬, 다양한 미분법, 로그함수, 시그모이드함수

 

📌 Matrix

행렬곱 : torch 사용시 모델의 레이어를 쌓을 때 shape을 맞춰주는 데에 주로 활용

Unit Matrix : 활성화함수로 활용하여 결과값이 그대로 출력되도록 활용

Transposed Matrix : 설명하기 편하도록 특징과 샘플의 구성을 수정할 때 활용

 

 

📌 Derivative

어느 한 점에서의 순간적인 변화율 ➡️ 기울기

모델의 오차를 줄여나가기 위해 활용

『

다양한 미분법 : 분수 미분, 편미분, 연쇄법칙 활용 多

』

 

 

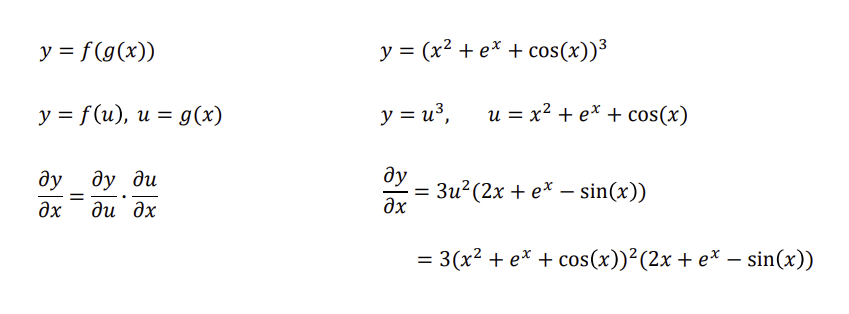
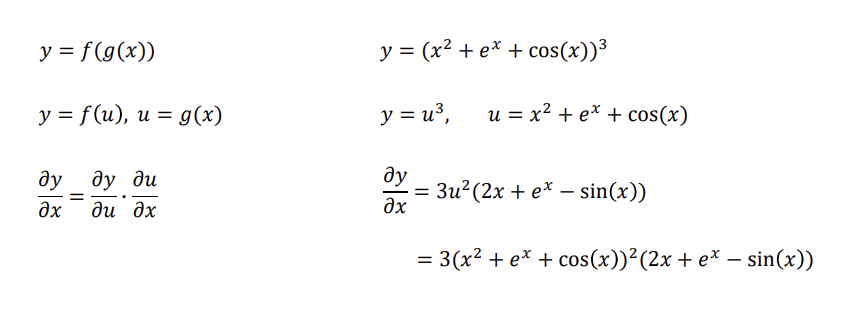
📌 Log Function

추후 배울 비용함수를 위해 형태와 특징정도 파악 필요

 

 

📌 Sigmoid Function

활성화함수로 사용하여 n 이상일 경우 1, 그렇지 않을 경우 0으로 판단 등에 활용

 

 

📌 Sigmoid Derivative

모델 학습에서 원하는 값이 나오지 않았을 경우, 과정을 돌아보며 기울기를 구하여 파라미터 조정의 근거로 활용 (각 네트워크 노드마다 시그모이드 함수가 붙는 경우 多)

 

 

📌 Partial Derivative

회귀함수를 wx+b로 두었을 때, 부분미분를 통한 y의 변화율 알아보기

: w에 따른 y의 변화율, b에 따른 y의 변화율을 구해 오차가 가장 적게끔 파라미터를 조정하는 데에 활용

『

⬇️ 시그모이드함수 부분미분 예시

』