[영상처리] Point Processes : Arithmetic Operations, Logical Operations, Look-up Table Processing
📌 Spatial domain processing
g(x, y) = T[f(x, y)]
f(x, y) : 원본이미지
g(x, y) : output 이미지
T[.] : 함수
📌 Point Processes
s = T(r)
r : gray-level of f(x, y)
s : gray-lavel of g(x, y)
T[.] : 아날로그 → 디지털 흑백 영상으로 만드는 함수
ex) a → b

이 외에도 다양한 Point Process 존재
- Arithmetic operations
- Logical operations
- Look-up table processing // 이번 게시글에서는 여기까지 다룸
- Histogram
- Contrast stretching
- Intensity transform
📌 Arithmetic operations
g(x,y) = f(x,y) + c
g(x,y) = a * f(x,y)
등과 같이, 산술 연산을 통해 밝기, 대비 등을 조절하는 연산
픽셀에 더하기 : 밝기 조절 (더하면 밝기가 높아지고 빼면 밝기가 낮아짐)
픽셀에 곱하기 : 대비조절 (곱하면 대비가 높아지고 나누면 대비가 낮아짐)
이때, 중요한 것은 밝기 범위(0~255)를 넘어가지 않도록 clamping 과정 필요
📌 Logical Operations
조건연산자를 동반하여 특정 내용을 특정 밝기로 변환하는 연산
ex) 입력 영상의 특정 밝기 값을 0으로 변환하라
if (f(x,y) > 120 and f(x,y) < 128) then g(x,y) = 0
📌 Look-up Table
1-dimensional array를 활용하여 밝기 값 변환
index : current pixel value
output(value) : generated new pixel value
[ 장점 ]
사용하기 쉬움 (소프트웨어: array, 하드웨어: memory)
복잡한 수학적 표현을 LUT 프로그래밍만으로 구현 가능 (예: y = sin x, y = log x)
[ 그래프 표현 ]
그래프로 표현할 때는 아래와 같이 x는 input값, y는 output값으로 표현

이런 함수를 어떻게 정의하냐에 따라 LUT는 다양한 변환을 낼 수 있음
[ Gamma correction ]
: 비선형 그래프로 밝기 변환
즉, 선형 변환의 경우 밝기가 일괄적으로 변환되지만, 감마 변환의 경우 감마 값에 따라 비선형 변환 수행
(이로써 0이 되는 구간이 많아지지 않고 자연스럽게 밝기를 조정할 수 있음)

gamma < 1 일 경우 어두운 영역의 변화폭이 크고 밝은 영역의 변화폭이 작음
즉, 밝은 영역이 급격하게 밝아지지 않은 채로, 어두운 영역만 잘 보임
gamma > 1 일 경우 밝은 영역의 변화폭이 크고 어두운 영역의 변화폭이 작음
즉, 어두운 영역이 급격하게 어두워지지 않은 채로, 밝은 영역만 잘 보임
- 🚨 문제점 -
R, G, B 별도의 감마 보정 필요
잘못된 감마 보정으로 인해 회색 이미지에 의도하지 않은 색상 신호가 생성될 수 있음
(각 디스플레이 장치에는 서로 다른 감마 특성이 있기 때문)
ex) CRT, PDP, LCD는 감마가 전혀 다름
카메라 신호는 감마 보정 신호를 렌더링
카메라가 감마 보정시, PDP에는 역감마 보정 필요
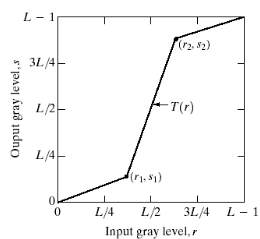
[ LUT를 사용한 이미지 enhancement ]
원 이미지가 대조가 작다면 (밝기가 중간 값에 몰려있음),
밝기 대응 선을 적절히 적용하여 밝기 범위 늘리기 (밝기의 누적 분포를 가로로 늘렸다고 보면 됨)
아래와 같이 같이 픽셀별 대응 함수를 통해 대조를 키울 수 있음


이 외에도 LUT를 활용해 특정 레벨만 보이게 하거나 특정 레벨을 없앨 수 있음
